Ventajas y desventajas

Kriging bayesiano empírico ofrece varias ventajas y desventajas en comparación con otros métodos de interpolación.

Estimación de semivariograma

A diferencia de otros métodos de kriging (que usan mínimos cuadrados ponderados), los parámetros del semivariograma en EBK se calculan usando la probabilidad máxima restringida (REML). Debido a las limitaciones computacionales de REML para datasets grandes, los datos de entrada se dividen primero en subconjuntos superpuestos de un tamaño especificado (valor predeterminado de 100 puntos por subconjunto). En cada subconjunto, los semivariogramas se estiman del siguiente modo:

1. Se estima un semivariograma a partir de los datos del subconjunto.
2. Usando este semivariograma como modelo, se simulan incondicionalmente datos nuevos en cada una de las ubicaciones de entrada del subconjunto.
3. Se estima un semivariograma nuevo a partir de los datos simulados.
4. Los pasos 2 y 3 se repiten el número de veces especificado. En cada repetición, el semivariograma estimado en el paso 1 se utiliza para simular un nuevo conjunto de datos en las ubicaciones de entrada y los datos simulados se utilizan para estimar un nuevo semivariograma.

Este proceso crea un gran número de semivariogramas para cada subconjunto, y cuando se trazan juntos, el resultado es una distribución empírica de semivariogramas sombreados por densidad (cuanto más oscuro es el color azul, más semivariogramas pasan por esa región). Las semivarianzas empíricas se representan mediante cruces azules. Además, la mediana de la distribución se colorea con una línea roja continua y los percentiles 25 y 75 se colorean con líneas rojas discontinuas, como se muestra a continuación.

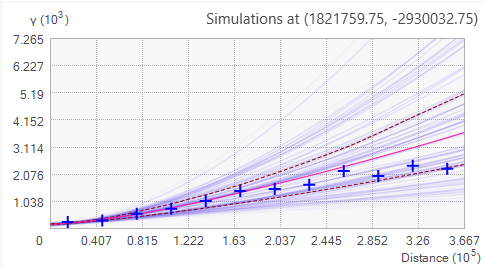
El número de semivariogramas simulados por subconjunto tiene el valor predeterminado de 100, y cada uno de estos semivariogramas es una estimación del verdadero semivariograma del subconjunto.

Para cada ubicación de predicción, la predicción se calcula usando una nueva distribución de semivariograma empírico que se genera fusionando los semivariogramas individuales a partir de las distribuciones del semivariograma en la vecindad del punto. Por ejemplo, si una ubicación de predicción tiene vecinos en tres subconjuntos (como se especifica en la vecindad de búsqueda), la predicción se calculará usando los semivariogramas simulados de cada uno de los tres subconjuntos. Los semivariogramas de cada subconjunto se ponderan según el número de vecinos que aportan a la predicción. Esto permite que los subconjuntos que aporten más vecinos tengan más influencia en el valor predicho.

Cuando se realiza Kriging bayesiano empírico en Geostatistical Wizard, puede ver los subconjuntos que se utilizaron para calcular el valor predicho. En la siguiente imagen, la ubicación de predicción es el centro del punto de mira de la vista previa de superficie. El círculo pequeño alrededor del punto de mira es la vecindad de búsqueda, y los dos polígonos grandes superpuestos muestran los puntos contenidos en los dos subconjuntos que se utilizaron para calcular la predicción. En este ejemplo, los puntos del centro del mapa se incluyen en ambos subconjuntos. Puede activar y desactivar estas visualizaciones de polígonos con el botón que indica la flecha:

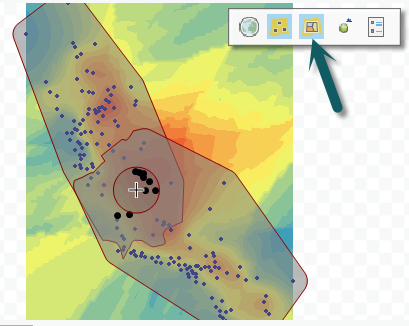
Modelo de kriging

Kriging bayesiano empírico se diferencia de otros métodos de kriging de Geostatistical Analyst por el uso de una función aleatoria intrínseca como modelo de kriging.

Otros modelos de kriging presuponen que el proceso sigue un valor medio general (o tendencia especificada) con variaciones individuales alrededor de este valor medio. Las desviaciones grandes se reducen hasta el valor medio, de modo que los valores nunca se desvían demasiado. Sin embargo, EBK no presupone una tendencia hacia un valor medio general, de modo que las desviaciones grandes tienen la misma probabilidad de ser más grandes como de ser más pequeñas. Por lo tanto, las funciones aleatorias intrínsecas corrigen inherentemente las tendencias de los datos.

Modelo de semivariograma

Para una distancia h dada, el kriging bayesiano empírico admite los siguientes semivariogramas:

• Potencia
  • γ(h)= nugget + b|h|^α
• Lineal
  • γ(h)= nugget + b|h|
• Spline de lámina delgada
  • γ(h)= nugget + b|h²|*ln(|h|)

nugget y b (pendiente) deben ser positivos, y α (potencia) debe estar entre 0,25 y 1,75. Con estas restricciones, los parámetros se estiman utilizando REML. Estos modelos de semivariogramas no tienen un parámetro de rango o meseta porque las funciones no tienen límite superior.

En EBK, es posible analizar la distribución empírica de las estimaciones del parámetro porque se estiman muchos semivariogramas en cada ubicación. Al hacer clic en las pestañas Nugget, Pendiente o Potencia, se muestran las distribuciones de los parámetros asociados. El siguiente gráfico muestra las distribuciones de los parámetros del semivariograma para los semivariogramas simulados mostrados en el gráfico anterior:

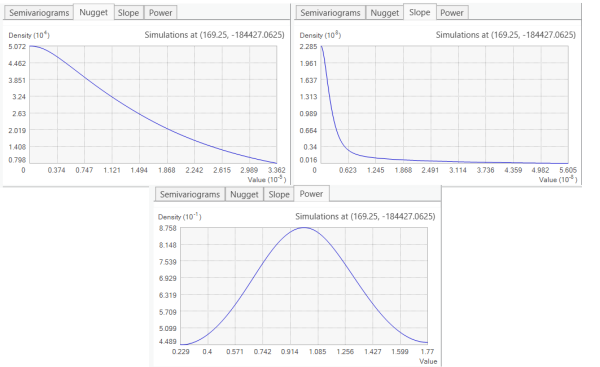
Al hacer clic en una ubicación diferente en la superficie de vista previa, se muestran la distribución del semivariograma y las distribuciones de los parámetros del semivariograma para la nueva ubicación. Si las distribuciones no cambian significativamente en el dominio de datos, sugiere que los datos son globalmente estacionarios. Las distribuciones deben cambiar suavemente a lo largo del dominio de datos; sin embargo, si ve cambios grandes en las distribuciones a lo largo de distancias pequeñas, incrementar el valor de Factor de superposición puede suavizar las transiciones de las distribuciones.

Nota:

Como se describe en la sección Transformaciones a continuación, al aplicar una transformación, el modelo de kriging cambia de una función aleatoria intrínseca a un modelo de kriging simple, y varios modelos de semivariogramas adicionales pasan a estar disponibles.

Transformaciones

El kriging bayesiano empírico ofrece la transformación de puntuación normal de sesgo multiplicativo con la opción de dos distribuciones base: Empírica y Empírica logarítmica. La transformación Empírica logarítmica requiere que todos los valores de datos sean positivos y garantiza que todas las predicciones sean positivas. Resulta adecuado para datos como las precipitaciones, que no pueden ser negativos.

Si se aplica una transformación, se utiliza un modelo de kriging simple en lugar de una función aleatoria intrínseca. Debido a estos cambios, las distribuciones de parámetros cambian a Nugget, Meseta parcial y Rango.

Si se elige K de Bessel o K de Bessel sin tendencia para Tipo de semivariograma, se mostrará un gráfico adicional para el parámetro Forma de K de Bessel. También aparece una pestaña Transformación adicional que muestra la distribución de las transformaciones ajustadas (una para cada simulación). Al igual que en la pestaña Semivariogramas, la distribución de la transformación está coloreada por densidad, y se proporcionan líneas de cuantiles.

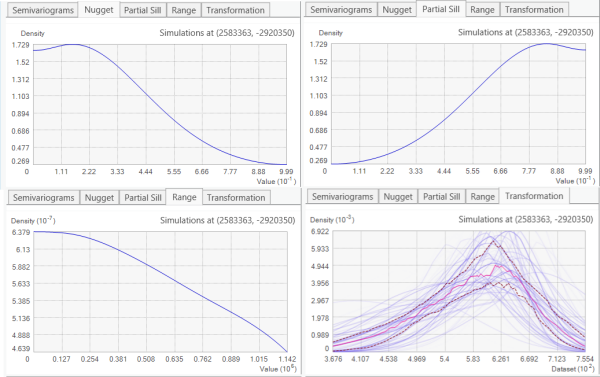
Semivariogramas

En todos los métodos de estadísticas geográficas se presupone una autocorrelación espacial, es decir, que las cosas más cercanas son más similares que las cosas que están más lejos, y el semivariograma define cómo disminuye la similitud con la distancia. En algunos semivariogramas (Exponencial, por ejemplo) se presupone que la similitud disminuye rápidamente. Por otro lado, el modelo de semivariograma Whittle presupone que la similitud disminuye lentamente. Incluso con el mismo nugget, rango y meseta, estos dos semivariogramas definirán la disminución de similitud de formas claramente diferentes. La clave para obtener resultados fiables es elegir el semivariograma que más se acerque al comportamiento del fenómeno. Los modelos de semivariogramas disponibles dependen de la transformación que elija.

Si Transformación se ha definido como Ninguna, estarán disponibles los siguientes modelos de semivariogramas:

• Potencia (predeterminado)
• Lineal
• Spline de lámina delgada

Si Transformación se ha definido como Empírica o Empírica logarítmica, estarán disponibles los siguientes modelos de semivariogramas:

• Exponencial (predeterminado)
• Exponencial sin tendencia
• Whittle
• Whittle sin tendencia
• K de Bessel
• K de Bessel sin tendencia

Los tres modelos de semivariogramas con eliminación de tendencia son los mismos que sus equivalentes directamente sin tendencia, excepto que se aplica una eliminación de tendencia de primer orden. La eliminación de la tendencia tiene un efecto insignificante en la velocidad de cálculo.

Elegir un semivariograma

La elección del semivariograma debería estar clara la mayoría de las veces, en función de los siguientes criterios:

• Si no le importa esperar para obtener los resultados más precisos, debería elegir K de Bessel o K de Bessel sin tendencia. La presencia o ausencia de tendencia debería determinar cuál de ellos.
• Si necesita resultados rápidos y no le importa perder cierta precisión, debería elegir Lineal o Spline de lámina delgada. Si no hay tendencia o la tendencia es débil, es mejor elegir Lineal.
• Si necesita un equilibrio entre precisión y velocidad, Potencia es una buena opción.
• Si se requiere una transformación, pero no puede permitirse esperar mucho tiempo para obtener la salida, debería elegir Exponencial o Whittle (o sus equivalentes sin tendencia). Debería elegir el que coincida mejor con las semivarianzas empíricas de Geostatistical Wizard (que se describe a continuación). También se debe tener en cuenta la validación cruzada.

Si está intentando elegir entre Exponencial, Whittle y sus equivalentes sin tendencia, debería elegir el semivariograma que proporcione el mejor ajuste visual a las semivarianzas empíricas (las cruces azules de los gráficos siguientes). Lo ideal es que las semivarianzas empíricas estén en la parte central del espectro del semivariograma. Por ejemplo, en el siguiente gráfico, las cruces azules no están en la parte central del espectro del semivariograma (la mayoría se encuentra hacia la parte superior del espectro):

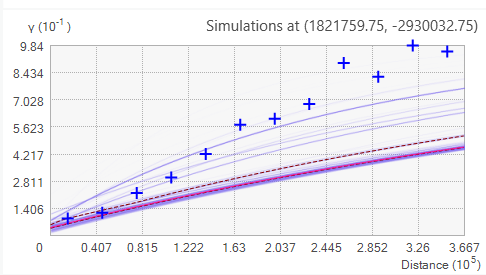
En su lugar, se debería preferir el siguiente semivariograma porque las cruces azules están en la parte central del espectro del semivariograma:

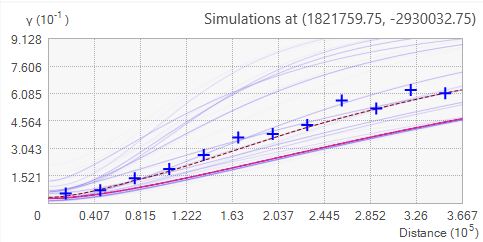
Cálculos de distancia para datos en coordenadas geográficas

Si los datos de entrada están en un sistema de coordenadas geográficas, las distancias se calcularán utilizando la distancia de cuerda. La distancia de cuerda entre dos puntos cualesquiera es la distancia en línea recta que conecta los dos puntos. Esta línea atravesará la Tierra en lugar de ir a lo largo de su superficie. Para visualizarlo, imagínese que ilumina con una linterna una esfera transparente. La longitud del haz de luz entre el punto por el que la luz entra y sale de la esfera es la distancia de cuerda entre estos dos puntos. La principal ventaja de utilizar la distancia cordal en lugar de la geodésica es que requiere menos potencia computacional. Además, solo existe teoría limitada sobre el uso de kriging en esferoides.

En versiones anteriores de ArcGIS se trataron las coordenadas geográficas como coordenadas cuadradas y se calculó la distancia euclidiana entre los puntos. Sin embargo, una celda de 1 grado por 1 grado no es realmente un cuadrado, por lo que esta distancia se distorsionará. Esta distorsión aumenta al moverse más al norte o al sur desde el ecuador.

Parámetros adicionales para el kriging bayesiano empírico

Kriging bayesiano empírico emplea tres parámetros que no aparecen en otros métodos de kriging:

• Número máximo de puntos de cada modelo local: especifica el número de puntos de cada subconjunto. Cuanto mayor sea el tamaño del subconjunto, más tiempo llevará calcular el EBK.
• Factor de superposición de área de modelo local: especifica el grado de superposición entre subconjuntos. Cada punto de entrada puede encontrarse en varios subconjuntos, y el factor de superposición especifica el número promedio de subconjuntos en los que se encontrará cada punto. Por ejemplo, un factor de superposición de 1,5 significa que aproximadamente la mitad de los puntos se utilizará en un subconjunto y la otra mitad se utilizará en dos subconjuntos. Un valor alto del factor de superposición hace que la superficie de salida sea más suave, pero también aumenta el tiempo de procesamiento.
• Número de semivariogramas simulados: especifica el número de semivariogramas que se simularán para cada subconjunto. Cuantas más simulaciones haya, las predicciones serán más precisas, pero el tiempo de procesamiento también aumentará.

Referencias

• Chilès, J-P. y P. Delfiner (1999). Capítulo 4 de Geostatistics: Modeling Spatial Uncertainty. Nueva York: John Wiley & Sons, Inc.
• Krivoruchko K. (2012). "Empirical Bayesian Kriging," ArcUser otoño de 2012.
• Krivoruchko K. (2012). "Modeling Contamination Using Empirical Bayesian Kriging," ArcUser otoño de 2012.
• Krivoruchko K. y Gribov A. (2014). "Pragmatic Bayesian kriging for non-stationary and moderately non-Gaussian data," Mathematics of Planet Earth. Proceedings of the 15^th Annual Conference of the International Association for Mathematical Geosciences, Springer 2014, pp. 61-64.
• Krivoruchko K. y Gribov A. (2019). "Evaluation of empirical Bayesian kriging," Spatial Statistics volumen 32. https://doi.org/10.1016/j.spasta.2019.100368.
• Pilz, J. y G. Spöck (2007). "Why Do We Need and How Should We Implement Bayesian Kriging Methods," Stochastic Environmental Research and Risk Assessment 22 (5):621–632.